La chronique de Miss Mouton (Partie 3)

Chère brebis esseulée, Cher agneau innocent, Cher bélier maladroit : Bonjour !

Aujourd’hui, tu as franchi un cap … que dis-je un cap, une péninsule ! Désormais, tu ne t’attardes plus à observer le noir, mais à détailler le non blanc. Car oui, la boucle bouscule tes certitudes, et enfin tu comprends que sans elle, sans moi, sans cette mystérieuse idée, ta vie n’a aucun sens, aucune substance, aucun goût. Et malgré la fureur des hommes, malgré ses faiblesses, malgré son intangibilité, elle continue d’inspirer chacun d’entre nous, et se trouve bien loin des discours rationnels et matérialistes que les biens pensants essaient de nous imposer. En réalité, les hommes ne supportent plus aucun discours rationnel: tout ce qui a fait le monde, tout ce qui a été beau et grand dans ce monde n’est jamais né d’un discours rationnel. Et une fois les limites du langage et de la réflexion atteintes, les biens pensants sont toujours revenus à la simplicité de la boucle.

Simplicité … Cette caractéristique revient souvent dans mes propos. Pourtant, l’art de la simplicité est un casse-tête de la complexité. Quelle belle forme que la boucle, réunissant à la fois deux notions antinomiques. Jusqu’à présent, nous avons vu ensemble l’omniprésence de la boucle, sa puissance, et comment elle nous contrôle. Mais nous n’avons jamais réellement étudié sa beauté, sa singularité, son originalité. Certes, nous avons chassé de notre esprit l’idée simpliste qu’il ne s’agissait que d’un vulgaire amas de fil arbitrairement disposé, mais nous n’avons pas eu le temps de dire ce qu’il en était réellement. Peut-être as-tu regretté ce manque. Aujourd’hui, ton désir va être comblé, car seul un être confirmé peut ressentir sa noblesse et son esthétique. Cet être confirmé, c’est toi !

Les lignes de ce jour ne te plairont probablement pas, malheureusement, je le regrette de tout mon coeur, mais nous n’avons pas le choix. Une fois cette étape passée, tu seras presque prêt à propager la bonne parole à mes côtés. La complexité … c’est bien de cela dont il va s’agir. Ou plus exactement des nombres complexes, grossièrement appelés nombres imaginaires. Oui, tu l’auras compris, ce paragraphe va traiter d’un pan mystérieux des mathématiques, mais je vais m’efforcer de vulgariser bouclement bien tout cela  afin de t’éviter des maux de têtes désagréables. Le capitalisme, le libéralisme et autre maladie ont été inventé pour bloquer ton raisonnement, pervertir volontairement ton esprit afin de t’empêcher d’accéder au repos éternel, d’accéder à ton indépendance car vois tu, une société hiérarchisée n’est possible que sur la base de la pauvreté et de l’ignorance. La boucle en viendra à bout, laisse moi donc t’initier à cette étrange notion.
Les nombres complexes ont été inventés pour permettre la résolution de n’importe quelle équation (je te mets au défi de résoudre x² + 1 = 0), et contrairement à un nombre réel, ils sont représentables dans le plan. Cette particularité, née dans un simple souci pratique, est à l’origine de la beauté de la boucle ! Attention, je ne dis pas que la beauté de la boucle n’existe que grâce à une invention humaine moderne, comme si moderne était le nec plus ultra du compliment. Comme si parlant d’une chose, on ne pouvait pas dire plus haut, plus définitivement haut que moderne. D’ailleurs, quiconque croit en la boucle ne croit pas aux valeurs qui régissent l’Art d’aujourd’hui… La loi du nouveau. La loi de la surprise… La surprise est une chose morte. Morte à peine conçue… La boucle étant apparue  bien avant la venue de l’home sur terre, il s’agit donc de ne pas mal interpréter mes propos. Non non non, mais l’on constate que l’homme ne tente de l’expliquer qu’avec l’une de ses plus belles inventions.

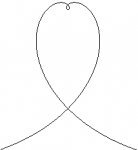
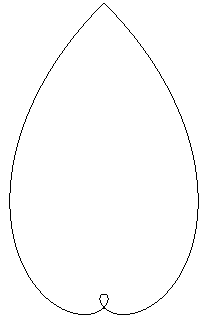Les deux boucles que tu peux voir sont une seule et même représentation du nombre imaginaire, noté i. Cette boucle est infinie, harmonieusement conçue. Elle s’enroule inlassablement, petit à petit, sur elle même et chacune des sous-surfaces crées est proportionnelle à toutes les autres. Prodigieux n’est-ce-pas ? La boucle n’est alors arrêtée que par la faiblesse des matériaux humains. Il s’agit simplement ici d’illustrer une notion fondamentale, que tu te dois de comprendre : la boucle, si belle, si élégante, est si puissante qu’elle domine également les mathématiques, et par là-même toute explication humaine. La notion d’infini est relative, l’esprit humain ne peut qu’évaluer, selon certaines conventions, un comportement infinitésimal. La boucle se définit elle comme étant intrinsèquement infinie, et sa forme la plus parfaite, le cercle, l’est d’autant plus qu’elle est à l’origine du nombre le plus obscur : pi.
Oh bien sûr, il serait possible à chaque fois d’étudier vulgairement chacune des boucles en notre possession. Cependant, il ne sera jamais possible pour l’être humain de l’expliquer concrètement, de prévoir son comportement, car cela fait appel à ces concepts encore inconnus, qui proviennent de l’infini et au delà! Mais je m’égare, et je vois bien dans tes yeux que cela ne te passionne pas.

Chère brebis esseulée, Cher agneau innocent, Cher bélier maladroit, la boucle est la réponse à la grande question de la vie, la boucle est la réponse. Comprendre cette infinité, c’est assurer la plénitude de ton âme. Tu te rends bien compte que tenter d’expliciter la boucle est une quête vouée à l’échec. Je ne t’apporte ici que quelques maigres éléments qui permettront, je l’espère, à ton esprit d’arriver aux bonnes conclusions. La boucle est ainsi esthétiquement réussie car inconcevable par l’esprit humain. La boucle est ainsi noble car sur un piédestal.

Je suis ton guide, ton humble serviteur. La fin est proche, te voilà bientôt maître ! La boucle vaut la peine d’être vécue, le bonheur est accessible, il suffit simplement de trouver sa vocation profonde, et de se donner à ce qu’on aime avec un abandon total de soi. La boucle est là pour toi !

Sengel
Miss Mouton